Question

Let g be a function that is defined for all x, x ≠ 2, such that g(3) = 4 and the derivative of g is

g′(x) = quotient of quantity x squared minus sixteen and x minus two with x ≠ 2.

Find all values of x where the graph of g has a critical value.
For each critical value, state whether the graph of g has a local maximum, local minimum, or neither. You must justify your answers with a complete sentence.
On what intervals is the graph of g concave down? Justify your answer.
Write an equation for the tangent line to the graph of g at the point where x = 3.
Does this tangent line lie above or below the graph at this point? Justify your answer.

Answer 1

1) x = ±4

2) For critical value x = -4, the graph of g has a local minimum as g''(-4) > 0. For critical value x = 4, the graph of g has a local minimum as g''(4) > 0.

3) There are no intervals for which the graph of g is concave down.

4) y = -7x + 25

5) Below the curve because the curve near point (3, 4) is concave up.

Explanation:

Given:

`g(x), \; x \\eq 2`

`g(3) = 4`

`g'(x)=(x^2-16)/(x-2)`

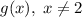
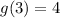
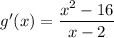
Question 1

The critical points of a function are the points where the derivative of the function is either zero or undefined.

Therefore, to find all values of x where the graph of g has a critical value, solve g'(x) = 0 and solve x - 2 = 0 (since a rational function is undefined when its denominator is zero).

`(x^2-16)/(x-2)=0`

`x^2-16=0`

`x^2=16`

`x=\pm4`

`x-2=0`

`x=2`

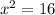
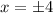
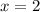
Note that x = 2 is not a critical point of g(x) since x = 2 is not in the domain of g.

Therefore, the critical points of the function g(x) are when x = ±4.

`\hrulefill`

Question 2

To determine the nature of the critical points, differentiate again to find the second derivative, g''(x).

• If g'(x) = 0 and g''(x) < 0, the point is a maximum.
• If g'(x) = 0 and g''(x) > 0, the point is a minimum.
• If g'(x) = 0 and g''(x) = 0, it could be a maximum, minimum or a point of inflection.

At a point of inflection, g''(x) = 0, but not all points where g''(x) = 0 are points of inflection. We need to determine what is happening on either side of the point to see if the sign of g''(x) is changing.

• If g''(x) > 0 on either side of a stationary point, the curve is convex (concave up) near the point, so it’s a minimum.
• If g''(x) < 0 on either side, the curve is concave (concave down), so it’s a maximum.
• If g''(x) changes sign, it’s a stationary point of inflection.

Find the second derivative g''(x) by using the quotient rule.

`\boxed{\begin{minipage}{5.5 cm}\underline{Quotient Rule for Differentiation}\\\\If $y=(u)/(v)$ then:\\\\$\frac{\text{d}y}{\text{d}x}=\frac{v \frac{\text{d}u}{\text{d}x}-u\frac{\text{d}v}{\text{d}x}}{v^2}$\\\end{minipage}}`

`\textsf{Let}\;\;u=x^2-16 \implies \frac{\text{d}u}{\text{d}x}=2x`

`\textsf{Let}\;\;v=x-2 \implies \frac{\text{d}v}{\text{d}x}=1`

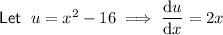
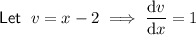
Therefore:

`g''(x)=(2x(x-2)-(x^2-16))/((x-2)^2)`

`g''(x)=(2x^2-4x-x^2+16)/((x-2)^2)`

`g''(x)=(x^2-4x+16)/((x-2)^2)`

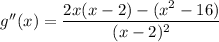
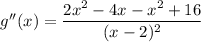
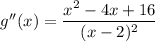
Substitute x = -4 and x = 4 into g''(x):

`g''(-4)=((-4)^2-4(-4)+16)/(((-4)-2)^2)=(4)/(3) > 0\implies \sf minimum`

`g''(4)=((4)^2-4(4)+16)/(((4)-2)^2)=4} > 0\implies \sf minimum`

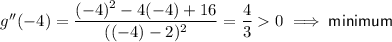
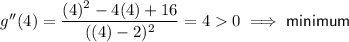
Therefore,

• For critical value x = -4, the graph of g has a local minimum as g''(-4) > 0.
• For critical value x = 4, the graph of g has a local minimum as g''(4) > 0.

`\hrulefill`

Question 3

A curve y = g(x) is convex (concave up) if g''(x) > 0 for all values of x.

A curve y = g(x) is concave (concave down) if g''(x) < 0 for all values of x.

Therefore, the graph of g is concave down for the values of x when:

`(x^2-4x+16)/((x-2)^2) < 0`

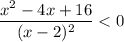
As x² - 4x + 16 > 0 for all values of x, and (x - 2)² ≥ 0 for all values of x, g''(x) is never less than zero. Therefore, there are no intervals for which the graph of g is concave down.

`\hrulefill`

Question 4

A tangent is a straight line that just touches the curve and has the same gradient (slope) as the curve at that point. The gradient (m) of the tangent line of the graph of g at point (x, y) is m = g'(x).

Therefore, to find the gradient of the tangent line to the graph of g at the point where x = 3, find g'(3):

`g'(3)=((3)^2-16)/((3)-2)=-7`

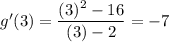
We know that g(3) = 4, so the point of tangency when the gradient of the tangent line is -7 is (3, 4).

To write the equation of the tangent line, simply substitute the found slope m = -7 and point (3, 4) into the point-slope form of a linear equation:

`\begin{aligned}y-y_1&=m(x-x_1)\\y-4&=-7(x-3)\\y-4&=-7x+21\\y&=-7x+25\end{aligned}`

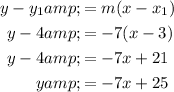
Therefore, the equation for the tangent line to the graph of g at the point where x = 3 is y = -7x + 25.

`\hrulefill`

Question 5

As the slope of the tangent line at (3, 4) is negative, the graph of g is decreasing around the point of tangency.

To determine if the tangent line lies above or below the graph of g at point (3, 4), substitute x = 3 and a value of x either side of x = 3 into g''(x) to determine its concavity near point (3, 4).

`g''(2.95)=((2.95)^2-4(2.95)+16)/(((2.95)-2)^2)=14.29...`

`g''(3)=((3)^2-4(3)+16)/(((3)-2)^2)=13`

`g''(3.05)=((3.05)^2-4(3.05)+16)/(((3.05)-2)^2)=11.88...`

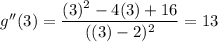
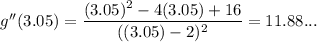
As g''(x) > 0 at and around (3, 4), the curve near point (3, 4) is concave up, so the tangent line will lie below the graph at this point.