I.
Given a function f with domain D and range R, and the inverse function
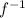
,
then the domain of
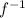
is the range of f, and the range of
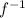
is the domain of f.
II. We are given the function
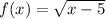
,
the domain of f, is the set of all x for which
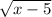
makes sense, so x is any x for which x-5
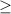
0, that is x≥5.
the range is the set of all values that f can take. Since f is a radical function, it never produces negative values, in fact in can produce any value ≥0
Thus the Domain of f is [5, ∞) and the Range is [0, ∞)
then , the Domain of
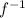
is [0, ∞) and the Range of
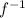
is [5, ∞)
III.
Consider
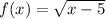
to find the inverse function
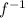
,
1. write f(x) as y:
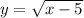
2. write x in terms of y:
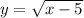
take the square of both sides
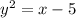
add 5 to both sides
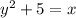
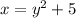
3. substitute y with x, and x with
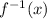
:

These steps can be applied any time we want to find the inverse function.
IV. Answer:

, x≥0
y≥0, where y are all the values that
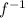
can take
Remark: the closest choice is B