Question

The area of a rectangle is greater than 10. What is a reasonable domain for the shorter side of the rectangle?

Answer 1

Let 'x' denote the longer side of the rectangle and let 'y' denote the shorter side of the rectangle.

From the problem, we know that:
x > y
xy > 10

With some rearranging, we get that:
x > y > 10/x

Answer 2

Explanation:

Given that area of a rectangle is greater than 10.

Normally length would be bigger than width

Let l = w+d where d is the difference between length and width

Then area
`=w(w+d) >10\\w^2+wd-10>0`

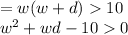
This is a quadratic equation and solution would be

`w=(-d±√(d^2+40) )/(2)`

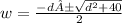
width cannot be negative

w>0

If square then l=w = \sqrt 10 = 3.162

Shortest side of the rectangle is

0<w<3.162

then only we have w shorter than length