Question

For which pair of functions f(x) and g(x) below will the limit as x goes to infinity of the product of f of x and g of x does not equal 0?

f(x) = 10x + e−x; g(x) =1 divided by the quantity 5 times x
f(x) = x2; g(x) = e−4x
f(x) =(Lnx)3; g(x) =1 divided by x
f(x) =square root of x; g(x) = e−x

Answer 1

the first function does not go to zero, all the others do.

Answer 2

let's check these folks using LH, or L'Hopital rule, since they're indeterminate types.


`\bf \textit{2nd pair listed gives }\\\\ \lim\limits_(x\to \infty)\ \cfrac{x^2}{e^(4x)}\implies \underline{LH}\quad \lim\limits_(x\to \infty)\ \cfrac{2x}{4e^(4x)}`

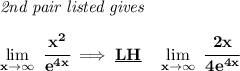
on this pair, the denominator is moving faster than the numerator, and thus, yielding a much larger denominator on every iteration, moving towards a limit of 0.


`\bf \textit{3rd pair listed gives }\\\\ \lim\limits_(x\to \infty)\ \cfrac{[ln(x)]^3}{x}\implies \underline{LH}\ \lim\limits_(x\to \infty)\ \cfrac{3ln(x)\cfrac{1}{x}}{1}\implies \lim\limits_(x\to \infty)\ \cfrac{3ln(x)}{x}`

on this pair, the denominator, again, is moving faster, since ln() results in an exponent for the constant "e", and thus is a much smaller then the denominator on every iteration, thus, the denominator gets much larger and moving towards 0 as limit as well.


`\bf \textit{4th pair listed gives }\\\\ \lim\limits_(x\to \infty)\ \cfrac{√(x)}{e^x}\implies \underline{LH}\lim\limits_(x\to \infty)\ \cfrac{(1)/(2√(x))}{e^x}\implies \lim\limits_(x\to \infty)\ \cfrac{1}{2e^x√(x)}`

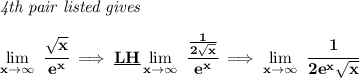
on this pair, the numerator is just a constant, thus is static, and the denominator is moving onwards on every iteration, thus moving also again towards 0.

now, let's take a peek of the 1st pair for f(x) and g(x)


`\bf \textit{1st pair listed gives }\\\\ \lim\limits_(x\to \infty)\ \cfrac{10+e^(-x)}{5x}\implies \underline{LH}\ \lim\limits_(x\to \infty)\ \cfrac{10-(1)/(e^x)}{5} \\\\\\ \textit{notice, the limit of each term, specifically of }(1)/(e^x)\textit{ goes to \underline{0}} \\\\\\ \textit{so the function turns to }\lim\limits_(x\to \infty)\ \cfrac{10-0}{5}\implies \boxed{2}`