Question

Determine algebraically whether the function is even, odd, or neither even nor odd.
f(x)=2/x^2

Answer 1

an even function can be reflected across the y axis and map onto itself
example: f(x)=x²
an easy test is
if a function is even, then f(-x)=f(x)

an odd function can be reflected about the origin and map onto itself
example: f(x)=x³
a functio is odd if f(-x)=-f(x)


assuming ya meant
`f(x)=(2)/(x^2)`

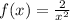
test the f(-x)=f(x) thing


`f(x)=(2)/(x^2)`

`f(-x)=(2)/((-x)^2)`

`f(-x)=(2)/(((-1)(x))^2)`

`f(-x)=(2)/((-1)^2(x)^2)`

`f(-x)=(2)/(1x^2)`

`f(-x)=(2)/(x^2)`

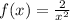
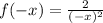
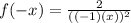
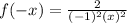
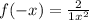
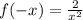
yep, same

it is even