Answer:
An obtuse triangle.
Explanation:
We have given the different sides of a triangle that is Side A = 2, Side B = 8 and Side C = 7.
According to the question, we can tell the triangle is acute, obtuse or a right triangle.
We know that,
For given sides x,y,z of a triangle,
If
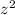 =
=
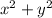 , then its a right triangle.
, then its a right triangle.
If
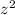 <
<
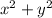 , then its an acute triangle.
, then its an acute triangle.
If
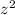 >
>
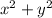 , then its an obtuse triangle.
, then its an obtuse triangle.
We have a = x = 2, b = z = 8 and c = y = 7.
Note: We always take z as the greatest side length.
Now,
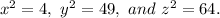
We can see that, 4 + 49 < 64.
So, we can apply rule
if
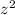 >
>
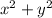 , then its an obtuse triangle.
, then its an obtuse triangle.
Therefore,
Given sides are of an obtuse triangle.