Question

Which of the following show the factored equivalent of f(x) = (x2 - 81)(x + 5) and its zeroes.

Answer 1

(x-9)(x+9)(x+5) has for zeroes: -9,-5,9

Answer 2

Factored form of function:
`f(x)=(x+9)(x-9)(x+5)`.

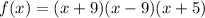Zeros of function:
`x=-9,-5,9`

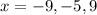
Explanation:

We have been given a function
`f(x)=(x^2-81)(x+5)`. We are asked to find the factored form and zeros of our given function.

Using difference of squares
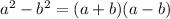`a^2-b^2=(a+b)(a-b)`, we can rewrite our given function as:

`f(x)=(x^2-9^2)(x+5)`

`f(x)=(x+9)(x-9)(x+5)`

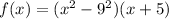
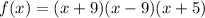
Therefore, the factored form of our given function is
`f(x)=(x+9)(x-9)(x+5)`.

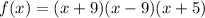To find the zeros of our given function, we will use zero product property. Upon equation our given function equals to zero we will get,

`(x+9)(x-9)(x+5)=0`

`(x+9)=0\text{ or }(x-9)=0\text{ or }(x+5)=0`

`x+9=0\text{ or }x-9=0\text{ or }x+5=0`

`x=-9\text{ or }x=9\text{ or }x=-5`

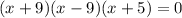
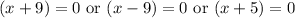
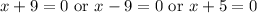
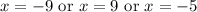
Therefore, the zeros of our given functions are
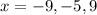`x=-9,-5,9`.