Step-by-step explanation
From the statement, we know that we have a right triangle that:
0. has an angle ∠C = 90°,
,
1. is also an isosceles triangle,
,
2. has a side AC = 3.
1) From points 2 and 3, we know that:
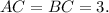
Because we have a right triangle, we can use Pitagoras Theorem, which states that:
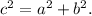
Where:
• c = AB = hypotenuse,
,
• a = BC = 3,
,
• b = AC = 3.
Replacing these data in the equation above, we get:
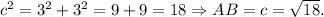
2) From point 2 we know that angles A and B must be equal:
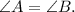
From geometry, we know that the inner angles of a triangle sum up to 180°, so we have:
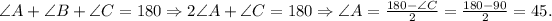
Where we have used point 1.
Answer
The sides of the triangle are:
• AB = √18,,
,
• AC = 3,
,
• BC = 3.
The angles of the triangle are:
• ∠A = 45°,,
,
• ∠B = 45°,,
,
• ∠C = 90°.