Question

What is the greatest common factor of the terms in the polynomial 12x4 + 2x3 –30x2? x x2 2x 2x2

Answer 1

12x^4 + 2x^3 - 30x^2

to find the GCF, lets first look at the coefficients.....the GCF of 12,2,and 30 is 2.

as for the variables....pick the one with the smallest exponent...and that would be x^2

so the GCF of this polynomial is 2x^2 <=

Answer 2

Option (4) is correct.

Greatest common factor of the given polynomial
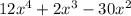`12x^4+2x^3-30x^2` is
`2x^2`

Explanation:

given polynomial
`12x^4+2x^3-30x^2`

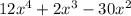
We have to find the greatest common factor of the terms in the given polynomial.

Greatest common factor is the largest number that is a factor of the each given term.

Consider the given polynomial
`12x^4+2x^3-30x^2`

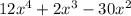
Here , the polynomial has three terms,

Prime factorization of given terms are,

`12x^4=2\cdot 2 \cdot 3 \cdot x \cdot x \cdot x \cdot x\\\\2x^3=2 \cdot x\cdot x\cdot x\\\\\-30x^2=-2 \cdot 3\cdot 5\cdot x\cdot x`

Thus, Greatest common factor
`2x^2`

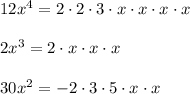
Thus, Greatest common factor of the given polynomial
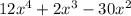`12x^4+2x^3-30x^2` is
`2x^2`

Thus, option (4) is correct.