Answer:
Rate of change of function in first 2 seconds is
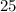 units per second.
units per second.
Explanation:
Average rate of change of a function is its gradient/slope (m)
Gradient or the rate of change can be calculated by the following equation,
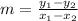
Here
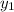 refers to a certain y axis value of the line drawn and
refers to a certain y axis value of the line drawn and
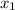 is the x value that corresponds to that y value.
is the x value that corresponds to that y value.
 and
and
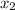 operates with same logic.
operates with same logic.
Lets pick a y value from the graph,
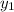 = 100
= 100
So the x value corresponding to that (
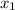 ) would be 2
) would be 2
Lets pick another y value from the graph.
[tex]y_{2}[/tex] = 50
So the x value corresponding to that (
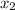 ) would be 0
) would be 0
So by substituting to the equation for gradient or the rate of change,
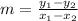
=
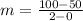
=

=
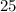
The graph is a linear graph so the rate of change of function is the same in every position.
Therefore the Rate of change of function in first 2 seconds is
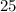 units per second.
units per second.