Question

Douglas has a segment with endpoints I(5, 2) and J(9, 10) that is divided by a point K such that IK and KJ form a 2:3 ratio. He knows that the distance between the x-coordinates is 4 units. Which of the following fractions will let him find the x-coordinate for point K?

2/3, 2/5, 3/2, 3/5

Answer 1

check the picture below.


`\bf \left. \qquad \right.\textit{internal division of a line segment} \\\\\\ I(5,9)\qquad J(9,10)\qquad \qquad 2:3 \\\\\\ \cfrac{I\underline{K}}{\underline{K} J} = \cfrac{2}{3}\implies \cfrac{I}{J} = \cfrac{2}{3}\implies 3I=2J\implies 3(5,9)=2(9,10) \\\\ -------------------------------\\\\`


`\bf { K=\left(\cfrac{\textit{sum of`

so. the x-coordinate of K will then be at
`\bf \cfrac{(3\cdot 5)+(2\cdot 9)}{2+3}`

----------------------------------------------------------------------------------------------


`\bf \cfrac{(3\cdot 5)+(2\cdot 9)}{2+3}\implies \cfrac{33}{5}\implies 6(3)/(5) \\\\\\ I(5,9)\impliedby \textit{to go from 5, to }6(3)/(5)\textit{ is just }1(3)/(5)\implies \cfrac{8}{5}\implies \cfrac{4\cdot 2}{5} \\\\\\ or\implies 4\cdot \cfrac{2}{5}\impliedby \textit{distance from 5 to }6(3)/(5)`

Answer 2

The correct option is 2.

Explanation:

It is given that the endpoints of the line segment are I(5, 2) and J(9, 10).

According to the section formula, if a point divide the line segment in m:n, then the coordinates of that point are

`((mx_2+nx_1)/(m+n),(my_2+ny_1)/(m+n))`

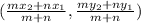
The x-coordinate is also written as

`x-coordinate=(m)/(m+n)(x_2-x_1)+x_1`

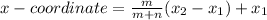
The distance between the x-coordinates is 4 units and
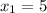`x_1=5`. So, the fractions that will let him find the x-coordinate for point K is

`(m)/(m+n)=(2)/(2+3)=(2)/(5)`

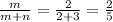
The required fraction is 2/5.

The x-coordinate of K is

`x-coordinate=(2)/(5)(4)+5=(33)/(5)`

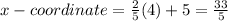
Therefore the correct option is 2.