Question

Stores on the verbal Graduate Record Exam (GRE) have a mean of 462 and a standard deviation of 119. Scores on the quantitative GRE have a mean of 584 and a standard deviation of 151. Assuming the scores are normally distributed, what quantitative scores are required for an applicant to score at or above the 90th percentile

Answer 1

We need Z-score here.

The formula is:

`z=(x-\mu)/(\sigma)`

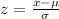
A normal curve (with 90th percentile), looks like the one below:

We need a standard normal table to move further.

When we go to the table, we find that the value 0.90 is not there exactly, however, the values 0.8997 and 0.9015 are there and correspond to Z values of 1.28 and 1.29, respectively

(i.e., 89.97% of the area under the standard normal curve is below 1.28).

The exact Z value holding 90% of the values below it is 1.282.

--------------- Now, we work backwords and find the value of x:

Verbal GRE:

`\begin{gathered} \mu=462 \\ \sigma=119 \\ z=(x-\mu)/(\sigma) \\ 1.282=(x-462)/(119) \\ x-462=1.282(119) \\ x=614.558 \end{gathered}`

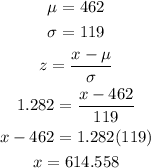
So, a 90th percentile on Verbal GRE is a score above 614.56

Quantitative GRE:

`\begin{gathered} z=(x-\mu)/(\sigma) \\ 1.282=(x-584)/(151) \\ x=777.582 \end{gathered}`

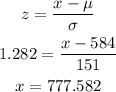
So, a 90th percentile on Quantitative GRE is a scoer above 777.58