Question

Marvin currently has a balance of $1192 in an account he has held for 14 years. he opened the account with an initial deposit of $800. what is the simple interest on the account?

a. 2.3%
b. 3.5%
c. 7.1%
d. 10.6%

Answer 1

`\bf \qquad \textit{Simple Interest Earned Amount}\\\\ A=P(1+rt)\qquad \begin{cases} A=\textit{accumulated amount}\to &1192\\ P=\textit{original amount deposited}\to& \$800\\ r=rate\to r\%\to (r)/(100)\\ t=years\to &14 \end{cases} \\\\\\ 1192=800(1+r14)\implies \cfrac{1192}{800}=1+14r\implies \cfrac{149}{100}=1+14r \\\\\\ \cfrac{149}{100}-1=14r\implies \cfrac{(149)/(100)-1}{14}=r`

you'd get a decimal value for the rate, just multiply it times 100, to get the percentage format of it.

Answer 2

Option B. 3.5%

Explanation:

Marvin currently has a balance of $1192 in his account. He opened the account with an initial amount of $800.

Duration for which the amount was held = 14 years

we have to calculate the rate of interest

Since Simple interest =
`\frac{\text{Principal amount* time* rate of interest}}{100}`

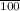
Interest = Final amount - initial amount

Interest = 1192 - 800

= $392

Now we plug these values in the formula

392 =
`(800* 14* R)/(100)`

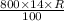
392 =
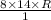
`(8* 14* R)/(1)`

R =
`(392)/(112)`

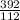
= 3.5%

Option B is the answer.