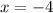Answer:
vertical asymptotes of the given function
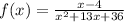 is
is
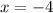 and
and

Explanation:
We have been given with the function
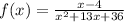 and we need to find the vertical asymptotes of the function
and we need to find the vertical asymptotes of the function
So, to find the vertical asymptotes we equate the denominator of given function to zero
we will get
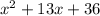 =0
=0
So, as to find the value of x we will factorise the above equation we will get
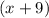 and
and
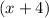
Hence, vertical asymptotes are at
 and
and