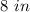Question

In a circle with an 8-inch radius, a central angle has a measure of 60°. How long is the segment joining the endpoints of the arc cut off by the angle?

Answer 1

The length of segment joining the endpoints of the arc is
`8\ in`

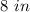
Explanation:

we know that

In the triangle ABC

see the attached figure to better understand the problem

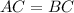`AC=BC` -----> is the radius of the circle

`m<CAB=m<CBA`

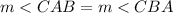
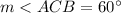`m<ACB=60\°` ----> given problem (central angle)

Initially the triangle ABC is an isosceles triangle

Remember that

the sum of the internal angles of triangle must be equal to
`180\°`

For this particular case, the isosceles triangle ABC becomes an equilateral triangle, as the three angles are equal to
`60\°`

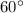
The equilateral triangle has three equal sides and tree equal angles

so

`AC=BC=AB`

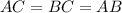
Hence

The length of segment joining the endpoints of the arc is
`8\ in`

Answer 2

calculate circumference first:

C = 2πr
C = 2(3.14159)(8 inches)
C = 50.265 inches

then 60/360 = 1/6 of the circle

50.265 inches / 6
= 8.378 inches (Round answer as needed)