Question

The diagram shows the curve y=(1/2x-2)^6+5. Find the area of the shaded region.

Answer 1

so the line that is the limit is where the equation crosses the y axis or where x=0

so
y=(1/2(0)-2)^2+5
y=(-2)^2+5
y=4+5
y=9
at y=9

the upper bound is y=9

alrighty

we will do
let's call the curve that is 6th degree f(x)
and the y=9, g(x)

f(x)=(1/2x-2)^6+5
g(x)=9

find where they intersect

9=(1/2x-2)^6+5
4=(1/2x-2)^6
fancy math
x=8

so the area under the curve will be

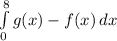
`\int\limits^8_0 {g(x)-f(x)} \, dx` because g(x) is above f(x)
so


`\int\limits^8_0 {g(x)-f(x)} \, dx= \int\limits^8_0 {9-(((1)/(2)x-2)^6+5)} \, dx=`
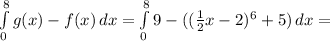
using our calculator because I can't figure out what
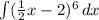
`\int\limits ((1)/(2)x-2)^6} \, dx` is

`\int\limits^8_0 {9-(((1)/(2)x-2)^6+5)} \, dx=`
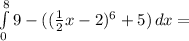
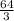
`(64)/(3)` or about 21.33333333