Question

Find the perimeter of the parallelogram shown.

35 yd
24 yd
26 yd
40 yd
1.07 Find the area of the parallelogram shown.
35 yd 2
24 yd 2
26 yd 2
40 yd 2
1.08 Wyatt’s dog is tethered to a post in his yard. If the rope tied to the dog is 12 feet
long, how many square yards does the dog have access to? (Use 3.14 for π.)
452.16 yd 2
50.24 yd 2
75.36 yd 2
25.12 yd 2
1.09 If the area of the following figure is 46 square centimeters, what is the height of the
trapezoid?
4 cm
2 cm
5.75 cm
3.1 cm

Answer 1

106-2*(8+5)=2*13=26
107- 7*5=35
108-12*12*3.14=452.16
109-(15+8)*h/2=46
23h=92
h=4

Answer 2

Option 3

Option 1

Option 1

Option 1

Explanation:

Given the sides of parallelogram 5 yd and 8 yd. Also height is 7 yd.

we have to find the perimeter and area of parallelogram.

As the opposite sides of parallelogram are equal and the perimeter is the sum of all the sides.

∴ Perimeter of parallelogram =5+8+5+8=26 yd.

Option 3 is correct.

`\text{Area of parallelogram=}Base* height=5* 7=35 yd^2`

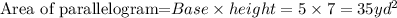
Option 1 is correct.

Given a rope tied to the dog 12 ft long. we have to find the area in square yards the dog have access.

`Area=\pi* r^2=(3.14)12^2=452.16 yd^2`

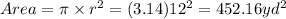
Option 1 is correct

Given a trapezoid and its parallel sides measures 8 cm and 15 cm and also area 46 sq centimeters. we have to find the height of the given trapezioid.

`\text{Area of trapezoid=}(1)/(2)*(\text{sum of parallel sides})* height`

`46=(1)/(2)* (8+15)* h`

⇒
`(42*2)/(23)=h`

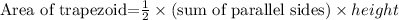
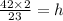
⇒ h=4 cm

Option 1 is correct.