Question

Options are 1183420 J730,575 J-452,845 J1183420 Ek730575 Ek-452,845452,845 J-730,575 J-118342p J

Answer 1

Given:

The initial speed of car is: u = 140 km/h = 140 × 5/18 m/s= 38.889 m/s

The final speed of the car is: v = 110 km/h = 110 × 5/18 m/s = 30.5556 m/s

The mass of the car is: m = 1565 kg

To find:

A) Initial kinetic energy of the car.

B) The final kinetic energy of the car.

C) Work done during the deceleration.

Step-by-step explanation:

A) The initial kinetic energy of the car can be calculated as:

`KE_i=(1)/(2)mu^2`

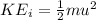
Substituting the values in the above equation, we get:

`\begin{gathered} KE_i=(1)/(2)*1565\text{ kg}*(38.889\text{ m/s})^2 \\ \\ KE_i=1183417.27\text{ J} \end{gathered}`

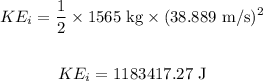
The value of initial kinetic energy is very close to the value 1183420 J given in the options. Thus, the initial kinetic energy of the car is 1183420 J.

B) The final kinetic energy of the car can be calculated as:

`KE_f=(1)/(2)mv^2`

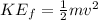
Substituting the values in the above equations, we get:

`\begin{gathered} KE_f=(1)/(2)*1565\text{ kg}*(30.5556\text{ m/s})^2 \\ \\ KE_f=730576.971\text{ J} \end{gathered}`

The value of final kinetic energy is very close to the value 730575 J given in the options. Thus, the final kinetic energy of the car is 730576 J.

C) The work done in the deceleration of the car is calculated by applying the work energy theorem. Thus, we get:

`\begin{gathered} W=KE_f-KE_i \\ \\ W=730575\text{ J}-1183420\text{ J} \\ \\ W=-452845\text{ J} \end{gathered}`

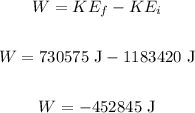
The work done in the deceleration of the car is -452845 J. The work done is negative because the car is decelerating.

Final answer:

A) The initial kinetic energy of the car is 1183420 J.

B) The final kinetic energy of the car is 730575 J.

C) The work done in decelerating the car is -452845 J.