Question

Webassign find the area of the region bounded by the parabola y = x2, the tangent line to this parabola at the point (6, 36), and the x-axis.

Answer 1

first find the tangent line

dy/dx=2x
at x=6, the slope is 2(6)=12
so
use point slope form
y-y1=m(x-x1)
point is (6,36)
so
y-36=12(x-6)
y-36=12x-72
y=12x-36

alright, so we know they intersect at x=6
and y=12x-36 is below y=x^2

so we do
`\int\limits^6_0 {x^2} \, dx - \int\limits^6_0 {12x-36} \, dx = \int\limits^6_0 {x^2-(12x-36)} \, dx = \int\limits^6_0 {x^2-12x+36} \, dx =`

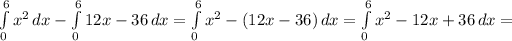
`[(x^3)/(3)-6x^2+36x]\limits^6_0=((6^3)/(3)-6(6)^2+36(6))-(0)=(216)/(3)-216+216=`
`72+0=72`

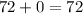
the area under the curve bounded by the lines and the x axis is 72 square units