Question

X = sin 1/2θ, y = cos 1/2θ, −π ≤ θ ≤ π(a) eliminate the parameter to find a cartesian equation of the curve.

Answer 1

First solve for theta in 'x' equation:

`\theta = 2 sin^(-1) x`

Substitute into 'y' equation:

`y = cos ((2 sin^(-1) x)/(2)) = cos (sin^(-1) x)`

Simplify by rewriting cos in terms of sine.
Using pythagorean identity:
`sin^2 + cos^2 = 1`


`cos = √(1-sin^2) \\ \\ y = \sqrt{1-sin^2 (sin^(-1) x)}`
Simplify using inverse function property:
`f(f^(-1) (x)) = x`


`y = √(1 - x^2)`

Answer 2

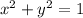`x^(2)+y^(2)=1` Standard form.

Explanation:

Parametric equations are useful to describe the motion of particles for instance, among other applications. In a trigonometric circle we can find its coordinates.

1) Rewriting for the sake of clarity:

`x=sin(1)/(2)\theta \:and\:\: y=cos(1)/(2)\theta \:,-\pi\leq \theta \leq \pi`

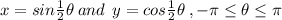
2) Solving, and using the Pythagorean Identity:

`x=sen(1)/(2)\theta ,y=cos(1)/(2)\theta \Rightarrow sen^(2)x+cos^(2)y=1\Rightarrow \left ( sen(1)/(2)\theta\right)^(2)+\left ( cos(1)/(2)\theta \right )^(2)=1\\\:Replacing\:the\:parameter\Rightarrow x^2+y^2=1`

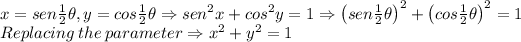
Since the value for
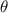`\theta` angle varies from
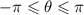`-\pi\leqslant\theta \leqslant \pi` then this is a description of a half of a circumference.

Check the graph below.