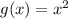Question

Find f(x) and g(x) so the function can be expressed as y = f(g(x)). y = (8/x^2) + 4

Answer 1

y=f(g(x)) and
`y= (8)/(x^(2))+4`


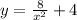
our aim is to express f as a function of g, where g is a function itself, of x.

in the expression tex]y= \frac{8}{x^{2}}+4 [/tex] we may notice 2 functions:

the squaring x function, which may well be our g:
`g(x)= x^(2)`

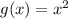
and the "8 divided by x, +4" function:
`f(x)= (8)/(x)+4`


check :


`f(g(x))= (8)/(g(x))+4`

because whatever the input of f is, it divides it from 8, and adds 4 to the division.

since,
`g(x)= x^(2)`,


`f(g(x))= (8)/(g(x))+4=(8)/(x^(2))+4`


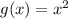
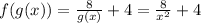
Answer:


`g(x)= x^(2)`


`f(x)= (8)/(x)+4`