Question

Based on the table of values below, find the slope between points where x = 1 and where x = 4.

X: 1 , 3 , 4
Y: 8, 6, -1

Answer Choices:
A. −3
B. Negative two thirds
C. Three over two
D. 3

Answer 1

Answer 2

The slope between the points where x=1 and where x=4 is :

-3

i.e. option: A is the correct answer.

Explanation:

Let Y=f(X)

We are given a table of values as:

X: 1 , 3 , 4

Y: 8, 6, -1

Let m represents the slope .

We know that the slope between the points x=a and x=b is give by:

`m=(f(b)-f(a))/(b-a)`

Here we are asked to find the slope between x=1 and x=4

i.e. we have:

a=1 and b=4

f(a)=8 and f(b)= -1

Hence, the slope between x=1 and x=4 is calculated as:

`m=(-1-8)/(4-1)\\\\m=(-9)/(3)\\\\m=-3`

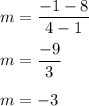
Hence, the slope is:

-3