Question

A ball is dropped from a height of 1600 meters. Each time the ban bouces, it reaches 3/4 of its original height. a) What are the first three terms of this sequence? b) Write an equation to represent this Sequence. c) Find the height of the ball after 4 bounces.

Answer 1

We know that

• The ball is dropped from 1600 meters high.

,

• Each time it bounces 3/4 of its original height.

This situation creates a geometric sequence where the reason is 3/4. To find the first three terms of this sequence, we just have to multiply each term with 3/4. We know that the first term is 1600.

`1600\cdot(3)/(4)=(4800)/(4)=1200`

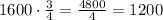
The second term is 1200 meters.

`1200\cdot(3)/(4)=(3600)/(4)=900`

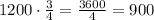
The third term is 900.

To find an equation, we have to use the geometric sequence formula-

`a_n=a_1\cdot r^(n-1)`

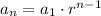
Replacing the information we have the equation that represents the situation of this problem.

`a_n=1600\cdot((3)/(4))^(n-1)`

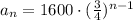
At last, the height after 4 bounces is

`900\cdot(3)/(4)=(2700)/(4)=675`

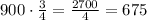
The height of the third bounce is 675 meters.

`675\cdot(3)/(4)=(2025)/(4)=506.25`

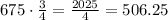
Therefore, the height of the ball after 4 bounces is 506.25 meters.