We know that
• The ball is dropped from 1600 meters high.
,
• Each time it bounces 3/4 of its original height.
This situation creates a geometric sequence where the reason is 3/4. To find the first three terms of this sequence, we just have to multiply each term with 3/4. We know that the first term is 1600.
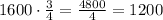
The second term is 1200 meters.
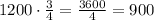
The third term is 900.
To find an equation, we have to use the geometric sequence formula-
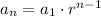
Replacing the information we have the equation that represents the situation of this problem.
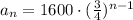
At last, the height after 4 bounces is
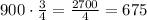
The height of the third bounce is 675 meters.
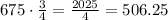
Therefore, the height of the ball after 4 bounces is 506.25 meters.