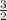Question

The sequence an = one half(2)n − 1 is graphed below:

coordinate plane showing the points 2, 1; 3, 2; 4, 4; and 5, 8

Find the average rate of change between n = 2 and n = 4.

three halves
two thirds
2
3
Please someone help me. Thank you.

Answer 1

your thing is very confusign

anyway, all I need to know to find the average rate of change from n=2 to n=4 is the value of (2,f(2)) and (4,f(4))

we see that the points are (2,1) and (4,4)
the average rate of change from n=2 to n=4 is the slope from (2,1) to (4,4)

slope between (x1,y1) and (x2,y2) is (y2-y1)/(x2-x1)
so slope between (2,1) and (4,4) is (4-1)/(4-2)=3/2
the slope is 3/2 or three halves


answer is three halves

Answer 2

option A is correct

three halves i.e,
`(3)/(2)`

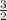
Explanation:

Average rate of Change(A(x)) of f(x) over interval [a, b] is given by:

`A(x) = (f(b)-f(a))/(b-a)`

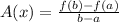
As per the statement:

The sequence is given as:

`a_n =(1)/(2) \cdot (2)^(n-1)`

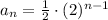
To find the average rate of change between n = 2 and n = 4.

From the coordinate plane:

At n =2

`a_2 = 1`

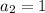
and

at n = 4

`a_4 = 4`

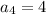
Now, using average formula we have;

`A(n) = (a_4-a_2)/(4-2)`

⇒
`A(n) = (a_4-a_2)/(2)`

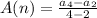
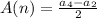
Substitute the given values we have;

`A(n) = (4-1)/(2) =(3)/(2)`

therefore, the average rate of change between n = 2 and n = 4 is,
`(3)/(2)`