Question

What are the dimensions of a rectangular box with a volume of 50b^3 + 75b^2 - 2b - 3?

(You don't need to explain it, I'm over that lol)

Answer 1

the factors are (5b - 1)(5b + 1)(2b + 3)
these are the 3 dimensions in terms of b

Answer 2

Answer: The dimensions are,

(5b+1) × (5b-1) × (2b+3)

Explanation:

Here, the given volume of the box,

`V=50b^3 + 75b^2 - 2b - 3`

`=25b^2(2b+3)-2b-3`

`=25b^2(2b+3)-1(2b+3)`

`=(25b^2-1)(2b+3)`

`=((5b)^2-(1)^2)(2b+3)`

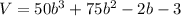
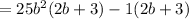
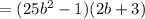
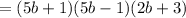`=(5b+1)(5b-1)(2b+3)` ( a² - b² = (a+b)(a-b) )

`\implies V=(5b+1)* (5b-1)* (2b+3)`.

Since, the volume of a rectangular box is,

V = l × w × h

Where l, w and h are the dimensions of the box.

By comparing,

The dimensions of the box are (5b+1) × (5b-1) × (2b+3)