Question

What is the slope of a line that is parallel to the line shown on the graph? A-4 B-1/4 C1/4 D4

Answer 1

just take any two points from the graph. For example (4, -2) , (0, -3) Slope = (y2-y1) / (x2-x1) = -2-(-3) / 4-0 = 1/4

Answer 2

Answer: The correct option is (C)
`(1)/(4).`

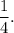
Step-by-step explanation: We are given to find the slope of a line that is parallel to the line shown on the graph.

We know that the slope of a line passing through the points (a, b) and (c, d) is given by

`m=(d-b)/(c-a).`

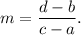
From the graph, we note that

the line passes through the points (0, -3) and (4, -2).

Therefore, the slope of the line on the graph is

`m=(-2-(-3))/(4-0)\\\\\\\Rightarrow m=(-2+3)/(4)\\\\\\\Rifhtarrow m=(1)/(4).`

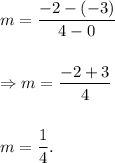
Thus, the slope of the line shown on the graph is
`(1)/(4).`

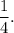
Option (C) is CORRECT.