Data:
Gummy bears: G
Chocolate kisses: C
G=50 ¢ a pound
C=30 ¢ a pound
97 pound mixture:
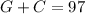
mixture worth € 35 (3500 ¢ ):
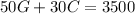
To find how much of each type of candy is in the mixture you use the next system of equations:
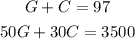
1. Solve one of the variables in one of the equations:
Solve G in the first equation:
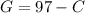
2. Use the value you find in the fisr part in the other equation:
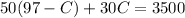
3. Solve the variable:
- Distributive property to remove the parenthesis:
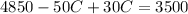
-Combine like terms:
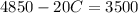
-Substract 4850 in both sides of the equation:

-Divide into -20 both sides of the equation:
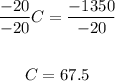
4. Use the value in part 3 to find the value of the other variable:
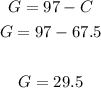
Then, the mixture has 29.5 pounds of gummy bears and 67.5 pounds of chocolate kisses