Question

At Marilyn's candy shop, she mixes gummy bears worth 50¢ a pound with chocolate kisses worth 30¢ a pound to create a 97 pound mixture worth 35€. To the nearest pound, how much of each type of candy is in the mixture?

Answer 1

Data:

Gummy bears: G

Chocolate kisses: C

G=50 ¢ a pound

C=30 ¢ a pound

97 pound mixture:

`G+C=97`

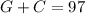
mixture worth € 35 (3500 ¢ ):

`50G+30C=3500`

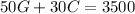
To find how much of each type of candy is in the mixture you use the next system of equations:

`\begin{gathered} G+C=97 \\ 50G+30C=3500 \end{gathered}`

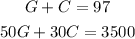
1. Solve one of the variables in one of the equations:

Solve G in the first equation:

`G=97-C`

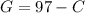
2. Use the value you find in the fisr part in the other equation:

`50(97-C)+30C=3500`

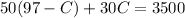
3. Solve the variable:

- Distributive property to remove the parenthesis:

`4850-50C+30C=3500`

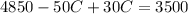
-Combine like terms:

`4850-20C=3500`

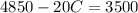
-Substract 4850 in both sides of the equation:

`\begin{gathered} 4850-4850-20C=3500-4850 \\ \\ -20C=-1350 \end{gathered}`

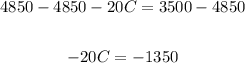
-Divide into -20 both sides of the equation:

`\begin{gathered} (-20)/(-20)C=(-1350)/(-20) \\ \\ C=67.5 \end{gathered}`

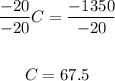
4. Use the value in part 3 to find the value of the other variable:

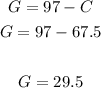
`\begin{gathered} G=97-C \\ G=97-67.5 \\ \\ G=29.5 \end{gathered}`Then, the mixture has 29.5 pounds of gummy bears and 67.5 pounds of chocolate kisses