Question

What values of a and b make the equation true? √648 = √2a.3b

Answer 1

We have:

648 : 2 = 324 (even number)
324 : 2 = 162 (even number)
162 : 2 = 81 (odd number)
81 : 3 = 27 (odd number)
27 : 3 = 9 (odd number)
9 : 3 = 3 (odd number)
3 : 3 = 1

So a = 3 and b = 4 - answer C.

Answer 2

Option (c) is correct.

a = 3 and b = 4

Explanation:

Given :
`√(648)=√(2^a\cdot3^b)`

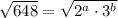
We have to find the values of a and b and choose the correct options from the given options.

Consider
`√(648)`

We first factorize 648 that is writing 648 as products of its prime factors.

648 can be written as 8 × 81

breaking 8 as product of 2 and 81 as product of 3.

We get,

`684=2^3* 3^4`

Also,

`√(648)=√(2^3\cdot3^4)`

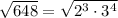
Thus, a = 3 and b = 4

Option (c) is correct.