Question

Which algebraic expression is a polynomial with a degree of 4?

5x4 + square root of 4x
x5 – 6x4 + 14x3 + x2
9x4 – x3 – x/5
2x4 – 6x4 + 14/x

Answer 1

C

Explanation:

• 5x4 + StartRoot 4 x EndRoot

• x5 – 6x4 + 14x3 + x2

• 9x4 – x3 – StartFraction x Over 5 EndFraction

• 2x4 – 6x4 + StartFraction 14 Over x EndFraction

Answer 2

A polynomial of degree n is an expression of the form:


`ax^(n)+bx^(n-1)+cx^(n-2)+...+dx^(2)+ex+f`

where a, b, c, ...d, e, f are Real numbers, and any of them can be = 0, except a.
and the degrees, n, n-1, .... are all non-negative integers: {0, 1, 2, 3 ...}


Among our choices,

the first one,
`5x^(4)+ √(4x)`,

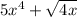
does not fit the polynomial definition, so the expression is not a polynomial.


the second one, is a fifth degree polynomial

the third one,
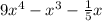
`9x^(4)-x^(3)- (1)/(5)x` is a fourth degree polynomial.

the fourth one,
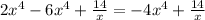
`2x^(4)-6x^(4)+ (14)/(x)= -4x^(4)+ (14)/(x)` is not a polynomial

Answer: 9x4 – x3 – x/5