Question

In how many different ways can a team of 3 boys and 2 girls be formed if there are 4 boys and 5 girls from which to select and Robert (one of the boys) must be on the team?

Answer 1

The selection of k object out of n, is done is C(n, k) many ways,

where,
`C(n, k)= (n!)/(k!(n-k)!)`

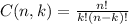
For example,

the selection of 2 objects out of 3, can be done in:


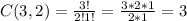
`C(3, 2)= (3!)/(2!1!)= (3*2*1)/(2*1)=3` many ways.

another example,

the selection of 2 objects out of 5 can be done in:


`C(5,2)= (5!)/(2!3!)= (5*4*3!)/(2!*3!)= (5*4)/(2)=10`

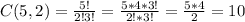
many ways.


back to our example,

there are C(3,2)=3 ways of selecting 2 boys out of 3, to form the 3 boys group together with Robert.

There are C(5,2)=10 many ways to select 2 girls out of 5.

Since any selection of the girls and boys can be combined, we have 3*10=30 different ways of forming the groups.


Answer: 30