Question

Btw the explanation is in words (example: because ? And ? are alternate interior angles, ? Is congruent to ?)

Answer 1

We know that ∠1 ≅ ∠4

As you determined ∠2 is the supplement of ∠1 and ∠3 is the supplement of ∠4, since ∠1 and ∠4 are equal, you can conclude that ∠2 and ∠3 are also equal.

Point R is the midpoint of XY, which indicates that it divides the line into two equal segments XR and RY.

Segment XR is formed by segments XP and PR, following the segment addition postulate you can determine that:

`XR=XP+PR`

Segment RY is formed by segments RT and TY, so that:

`RY=RT+TY`

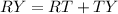
Following the substitution postulate, if XR and RY are equal, then:

`XP+PR=RT+TY`

We know that XP ≅ TY, sp they can be simplified from the sums and we get that:

`PR=RT`

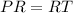
Finally, ∠QRP and ∠SRT are at opposite sides of the X shape formed by the intersection of lines QS and PT, they share a vertex at point R. These angles are vertically opposite angles and therefore congruent, so that:

`\angle\text{QRP}\cong\angle SRT`

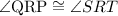
You can conclude that ΔPQR and ΔTSR are congruent by the Angle-Side-Angle postulate.