Question

Where are the x-intercepts for f(x) = −4cos(x − pi over 2) from x = 0 to x = 2π?

Answer 1

The function is
`f(x)=-4cos( x-( \pi )/(2) )`,

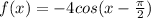
the x-intercepts of the function are the values of x, for which f(x)=0.

So we solve
`-4cos( x-( \pi )/(2) )=0`, where x∈[0,2π]


`-4cos( x-( \pi )/(2) )=0`


`cos( x-( \pi )/(2) )=0`


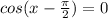
CosA=0, when A is
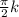
`( \pi )/(2) k`, where k is an integer.

-------------------------------------------------------------------------------------------------
check the unit circle, the cosine, that is the first coordinate, is 0 at 90°, that is π/2, at 270°, that is π/2*3
-------------------------------------------------------------------------------------------------

thus,


`x-( \pi )/(2)` is an element of
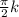
`( \pi )/(2) k`, that is


`{...-2*( \pi )/(2), -1*( \pi )/(2), 0*( \pi )/(2), 1*( \pi )/(2), 2*( \pi )/(2), 3*( \pi )/(2)...}`

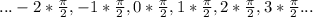
that is


`{...- \pi , -( \pi )/(2), 0, ( \pi )/(2), \pi , ( 3\pi )/(2), 2 \pi ...}`

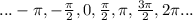
this means that x is an element of:


`{...- \pi+( \pi )/(2) , -( \pi )/(2)+( \pi )/(2), 0+( \pi )/(2), ( \pi )/(2)+( \pi )/(2), \pi+( \pi )/(2) , ( 3\pi )/(2)+( \pi )/(2), 2 \pi+( \pi )/(2) ...}`

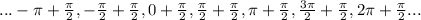
so x is an element of


`{...-( \pi )/(2) , 0, ( \pi )/(2), \pi , ( 3\pi )/(2) , 2 \pi,...}`

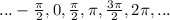
Since x can be from x=0 to x= 2π,

then the solution set is {0, π/2, π, 3π/2, 2π}


Answer: {0, π/2, π, 3π/2, 2π}