Question

Use the discriminant to describe the roots of each equation. Then select the best description. x2 - 5x + 7 = 0

Answer 1

The general form of a quadratic (second degree) equation is


`a x^(2) +bx+c=0`, where


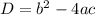
`D= b^(2)-4ac` is called the Discriminant.


The Discriminant determines how many roots the equation will have as follows:

i) if D>0, the equation has 2 roots.
ii) if D=0, the equation has 1 double root.
iii) if D<0, the equation has no roots.


In our equation,
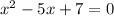
`x^(2) -5x+7=0`, a=1, b=-5, c=7

so the discriminant is D=(-5)^2-4*1*7=25-28<0


Thus the equation has no roots.


Remark: the equation has no roots in the Real numbers, but it has 2 roots in a larger set of numbers to be discussed in the future, the Complex numbers.