Answer:
Given the paint flow can be expressed with the function as:
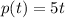
where, t represents time in minutes and p represents how far the paint is spreading.
It is also given that: The flowing paint is creating a circular pattern on the tile
The area of the pattern can be expressed as:
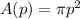
A
To find the area of the circle of spilled paint as a function of time.
![A[p(t)] = A[5t]](https://img.qammunity.org/2018/formulas/mathematics/high-school/ty4kcygvyy8f6loaj3i87sccbgm86eev0k.png)
⇒
![A[5t] = \pi \cdot (5t)^2 = 25 \pi t^2](https://img.qammunity.org/2018/formulas/mathematics/high-school/vu4hm1xq5lx724pq9hngd7c8xu1imkepnb.png)
therefore, the area of the circle of spilled paint as a function of time
![A[p(t)] = 25 \pi t^2](https://img.qammunity.org/2018/formulas/mathematics/high-school/p6krtrabczjsel9jp82spsc5qhjvinzw6j.png) . ......[1]
. ......[1]
B
To find how large is the area of spilled paint after 2 minutes.
Substitute t = 2 minutes and
 in [1] we have;
in [1] we have;
![A[p(2)] = 25 \cdot 3.14 \cdot 2^2 = 100 \cdot 3.14 = 314](https://img.qammunity.org/2018/formulas/mathematics/high-school/esj1d2hzomt6n0zt9d4zfd1pomk4u40jez.png) square units.
square units.
Therefore, 314 square units large is the area of spilled paint after 2 minutes.