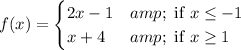Answer:
The piecewise function is
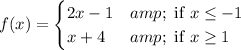
Explanation:
From the given graph it is noticed that the graph is divides into two pieces.
The first function is defined for all values of x which are less than or equal to -1. The second function is defined for all values of x which are greater than or equal to 1.
The equation of line which passing through two points is
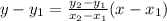
The first line is passing trough (-1,-3) and (-2,-5).
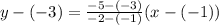
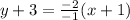
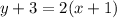
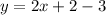
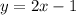
For
 the function is defined as,
the function is defined as,
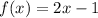
Similarly the second line is passing through (1,5) and (2,6).

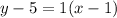
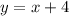
For
 the function is defined as,
the function is defined as,
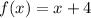
Therefore, the piecewise function is,