Question

Suppose the population of a town is 2,700 and is growing 4% each year.

a. Write an equation to model the population growth.

b. Predict the population after 12 years.

Answer 1

Part A
Y (x)=2700 (1+0.04)^x
Y (x)=2700 (1.04)^x
where x is the number of years

Part B
Y (12)=2,700×(1.04)^(12)=4,322.78
Round your answer to get 4323

Answer 2

a.
`y=2,700(1.04)^x`

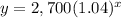
b. 4,322.

Explanation:

a. We have been given that the population of a town is 2,700 and is growing 4% each year.

We can see that population of town is increasing exponentially. Since an exponential function is in form:
`y=a*b^x`, where,

a = Initial value.

b= For growth b is in form (1+r), where r is rate in decimal form.

`y=a*(1+r)^x`

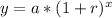
Let us convert our given rate in decimal form.

`4\%=(4)/(100)=0.04`

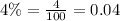
Upon substituting a=2,700 and r=0.04 we will get,

`y=2,700(1+0.04)^x`

`y=2,700(1.04)^x`

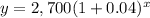
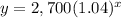
Therefore, the equation
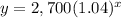`y=2,700(1.04)^x` models the population growth.

b. To find the population after 12 years we will substitute x=12 in our population growth model.

`y=2,700(1.04)^12`

`y=2,700*1.6010322185676808`

`y=4,322.78699013273816\approx 4,322`

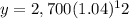
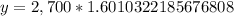
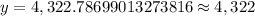
Therefore, the population after 12 years will be 4,322.