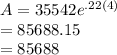Answer:
Explanation:
Clinton city was hit by an epidemic and hence population was declining 22% every hour
Let t be the no of hours after epidemic and A, the initial population at the start of epidemic
Then
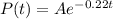
Also given that P(4) = 35542
We have to calculate A from this
Substitute t =4 and P (4) = 35542