Question

From a boat on the lake, the angle of elevation to the top of a cliff is 15°54'. If the base of the cliff is 967 feet from the boat how high is the cliff to the nearest foot?

Answer 1

tan 15 54 = h / 967

h = 967 * tan 15 54

= 275 feet to nearest foot

Answer 2

Height of the cliff is 188 feet.

Explanation:

Let us draw a diagram for the given situation.

In the diagram,

AB = cliff with base at B

C is the position of boat.

Hence, BC = 967.

∠C = 15°54' = 15.9°

In triangle ABC, we have

`\tan C=(AB)/(BC)\\\\\tan 15.9=(x)/(967)\\\\x=967\tan 15.9\\\\x=188.01`

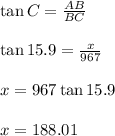
Hence, in nearest foot, the height of the cliff is 188 feet.