Question

The mean sat verbal score is 486, with a standard deviation of 95. use the empirical rule to determine what percent of the scores lie between 391 and 486. (assume the data set has a bell-shaped distribution.)

Answer 1

Answer: 34%

Step-by-step explanation: I’m smart

Answer 2

Find the z-scores for the two scores in the given interval.


`z=(x-\mu)/(\sigma)`

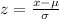
For the score x =391,
`z=(391-486)/(95)=(-95)/(95)=-1`.

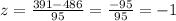
For the score x = 486,
`z=(486-486)/(95)=0`

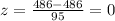
Now you want the area (proportion of data) under the normal distribution from z = -1 to z = 0. The Empirical Rule says that 68% of the data falls between z = -1 to z = 1. But the curve is symmetrical around the vertical axis at z = 0, so the answer you want is HALF of 68%.