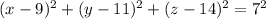Question

Find an equation of the largest sphere contained in the cube determined by the planes x = 2, x = 16; y = 4, y = 18; and z = 7, z = 21.

Answer 1

The x-coordinate of the center of the sphere is the midpoint of x=2 and x=16, that is (2+16)/2=18/2=9.

The y-coordinate of the center of the sphere is the midpoint of y=4 and y=18, that is (4+18)/2=22/2=11.

The z-coordinate of the center of the sphere is the midpoint of z=7 and z=21, that is (7+21)/2=28/2=14.


We also notice that the side lengths of the cube are:16-2 = 18-4 = 21-7 = 14

Thus, we have a sphere centered at (9, 11, 14) and radius R=14/2=7 units.


The equation of the sphere with radius R and center
`(x_0, y_0,z_0)` is given by:


`(x-x_0)^(2)+ (y-y_0)^(2)+ (z-z_0)^(2)= R^(2)`

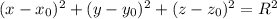
Thus the equation of the largest sphere contained in the box is:


`(x-9)^(2)+ (y-11)^(2)+ (z-14)^(2)=7^(2)`