Question

How are the distance formula and the pythagorean theorem related to one another?

Answer 1

here is the pythagorean theorem
a²+b²=c²
a and b are the lengths of the leg and c is the length of the hyptonuse

here is the distance formula

the disatnce beetween (x1,y1) and (x2,y2) is

`D=√((x_2-x_1)^2+(y_2-y_1)^2)`




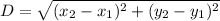
compare them both
c²=b²+a²

`D=√((x_2-x_1)^2+(y_2-y_1)^2)`

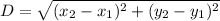
it seems that if we took the square root of both sides of the pythagorean theorem, we get something close to the distance formula
x2-x1 is the distance betwween the x values (1 leg) and y2-y1 is the distance bewteen the other 2 points (other leg)


think of it like this:
(x1,y1) and (x2,y1) are the 2 points of a right triangle that are not on the right angle
the length of the bottom leg or base is x2-x1 or x1-x2, it doesn't matter because it will be squared anyway
the length of the vertical leg is y2-y1 or y1-y2, it doesn't matter because the value will be squraed anyway

then we do pythaogreaon theorem to get the disatnce

Answer 2

they are the same because the distance formula depends on a right triangle relationship between x and y, where as the right triangle has the same relationship with x being one leg of the right triangle and y the other leg of the right triangle