The first one is a disjunction, an "or", meaning that the solution set shares no numbers on the number line. That's how you graph these...on a number line. Solving the first one, multiply both sides by 8 to get
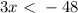
and divide to get x<-16. Now the second one, just divide both sides by 5 to get
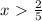
On a single number line, make 0 your center, put -16 where it belongs in reference to the 0 and put 2/5 where it belongs in reference to the 0. The numbers to the left of -16 are those that are less than -16, and the circle above the -16 is an open one, not including the -16. The numbers to the right of 2/5 are those numbers that are greater than 2/5, so put an open circle above the 2/5 and go to the right with that line. And you can see that you have a big open space between the -16 and the 2/5 where the solution set is not the same at all. For b, solve this one simultaneously. It is a conjunction, an "and", where there will be a solution set that is shared by both values for x. Solve it like this...start by subtracting 10 from both sides:
-8< -4d < -4 Now, when you divide by the negative 4, you have to change the signs to greater than: 2 > d > 1. That means, in words, that "d is less than 2 and greater than 1". On a single number line you will have open circles above the 1 and the 2 and the numbers in between 1 and 2 are shared solutions.