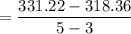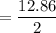Question

Jack invested some money in a bank at a fixed rate of interest compounded annually. The equation below shows the value of his investment after x years: f(x) = 300(1.02)x. What was the average rate of change of the value of Jack's investment from the third year to the fifth year?

Answer 1

The value of his investment at the third year is
F (3)=300×(1.02)^(3)=318.36

The value of his investment at the fifth year is
F (5)=300×(1.02)^(5)=331.22

The average rate of change of the value is
(331.22−318.36)÷2 years=6.43 per year

Answer 2

The average rate of change of Jack's investment from the third year to the fifth year is $6.43

Explanation:

The function that defines the value of his investment after x years,

`f(x)=300(1.02)^x`

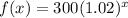
Putting the value of x as 3 and 5, we can get the value of his investment after 3 years and 5 years respectively.

So,

`f(3)=300(1.02)^3=318.36`

`f(5)=300(1.02)^5=331.22`

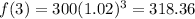
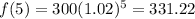
Then,

`\text{Average rate of change}=(f(x_2)-f(x_1))/(x_2-x_1)`

`=(331.22-318.36)/(5-3)`

`=(12.86)/(2)`

`=\$6.43`