Answer:
The difference of the values of the first and third quartiles of the data set is 6.
Explanation:
Data : 10, 9, 6, 12, 4, 6, 7, 8, 15, 14, 12, 9, 10, 5
This data set represents the number of cups of coffee sold in a café between 8 a.m. and 10 a.m. every day for 14 days.
Arrange the data in the ascending order :
4,5,6,6,7,8,9,9,10,10,12,12,14,15
No. of observations n = 14(even)
Median =
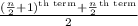
So, Median =
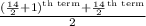
Median =
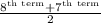
Median =
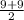
Median =

Median = 9
Now to find
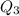 i.e. Third quartile
i.e. Third quartile
Consider the set of values right to the median .
9,10,10,12,12,14,15
Now find the median of this data
No. of observations n = 7(odd)
So, Median =

=
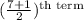
=

=
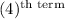
=
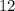
So,

Now to find
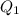 i.e. First quartile
i.e. First quartile
Consider the set of values left to the median .
4,5,6,6,7,8,9
No. of observations n = 7(odd)
So, Median =

=
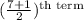
=

=
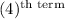
=

So,
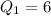
Now The difference of the values of the first and third quartiles of the data set : 12-6=6
Hence The difference of the values of the first and third quartiles of the data set is 6