Answer:
Part A -
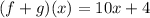
Part B -

Part C -
![f[g(x)]=16x-31](https://img.qammunity.org/2018/formulas/mathematics/high-school/hkwvss5rrxtfom6pjrs74gfn2rpyktdmzi.png)
Explanation:
Given : Functions
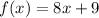 and
and
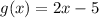
To find : Complete the function below :
Part A : (f+g)(x)
As
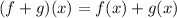
Substitute the value of f(x) and g(x)
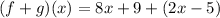
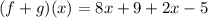
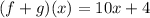
Part B : (f ⋅ g)(x)
As
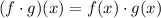
Substitute the value of f(x) and g(x)
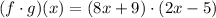



Part C : f[g(x)]
f[g(x)] means substitute value of g(x) in place of x in f(x)
![f[g(x)]=f[2x-5]](https://img.qammunity.org/2018/formulas/mathematics/high-school/lyeo2urh407n1n8b8zycyyrx8jdiwigarv.png)
![f[g(x)]=8(2x-5)+9](https://img.qammunity.org/2018/formulas/mathematics/high-school/lq8kw40e7xnj7oxskcrfzf6k7rv1p0ne0z.png)
![f[g(x)]=16x-40+9](https://img.qammunity.org/2018/formulas/mathematics/high-school/stln8cql254wnxcabh5jssq740bcphlmcx.png)
![f[g(x)]=16x-31](https://img.qammunity.org/2018/formulas/mathematics/high-school/hkwvss5rrxtfom6pjrs74gfn2rpyktdmzi.png)