Question

Find the center of a circle with the equation:
x2+y2−4x+2y−11=0

Answer 1

The center of a circle with the equation given is (2,-1).

Answer 2

The standard form for the equation of a circle is


`(x-h)^2+(y-k)^2=r^2`

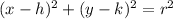
The center of such a circle is the point with coordinates (h, k).

To get your equation into that form, you have to complete the square (twice; once for x and once for y).

Add 11 to both sides so the constant appears on the right. Build in some space to add a couple of numbers, like this:


`x^2-4x+()+y^2+2y+()=11`

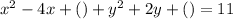
To complete the square on x, look at the coefficient of x (that's -4), take half of it (that's -2), then square it (that's 4). Add 4 inside the first pair of (). Do the same kind of thing for y -- half of 2 is 1 and 1 squared is 1; add 1 inside the second pair of (). Be sure to add 4 and 1 to the right side, too.


`x^2-4x+4+y^2+2y+1=16`

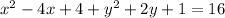
The first three terms factor and the next 3 terms factor.


`(x-2)^2+(y+1)^2=16`

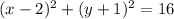
Match this up with the standard form


`(x-h)^2+(y-k)^2=r^2`

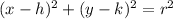
The center of the circle is (2, -1).