Given:
The trigonometric function is given as,

The objective is to simplify the expression.
Step-by-step explanation:
The given expression can be written as,
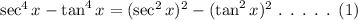
Now, consider the algebraic identity,
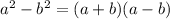
Then, the equation (1) can be written using the algebraic identity as,
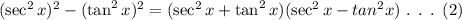
Consider the Pythagorean identity,
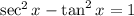
Then, equation (2) can be written as,
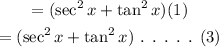
Hence, the simplified expression is sec²x + tan²x.