Question

How do I solve this problem?By using the pythagorean identities. The answer should be in a form of for example Cosx.

Answer 1

Given:

The trigonometric function is given as,

`\sec ^4x-\tan ^4x`

The objective is to simplify the expression.

Step-by-step explanation:

The given expression can be written as,

`\sec ^4x-\tan ^4x=(\sec ^2x)^2-(\tan ^2x)^2\text{ . . . . . (1)}`

Now, consider the algebraic identity,

`a^2-b^2=(a+b)(a-b)`

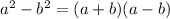
Then, the equation (1) can be written using the algebraic identity as,

`(\sec ^2x)^2-(\tan ^2x)^2=(\sec ^2x+\tan ^2x)(\sec ^2x-tan^2x)\text{ . . . (2)}`

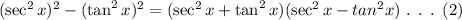
Consider the Pythagorean identity,

`\sec ^2x-\tan ^2x=1`

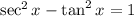
Then, equation (2) can be written as,

`\begin{gathered} =(\sec ^2x+\tan ^2x)(1) \\ =(\sec ^2x+\tan ^2x)\text{ . . . . . (3)} \end{gathered}`

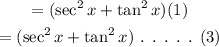
Hence, the simplified expression is sec²x + tan²x.